Forme factorisée \( f(x) = a(x-x_1)(x-x_2) \)
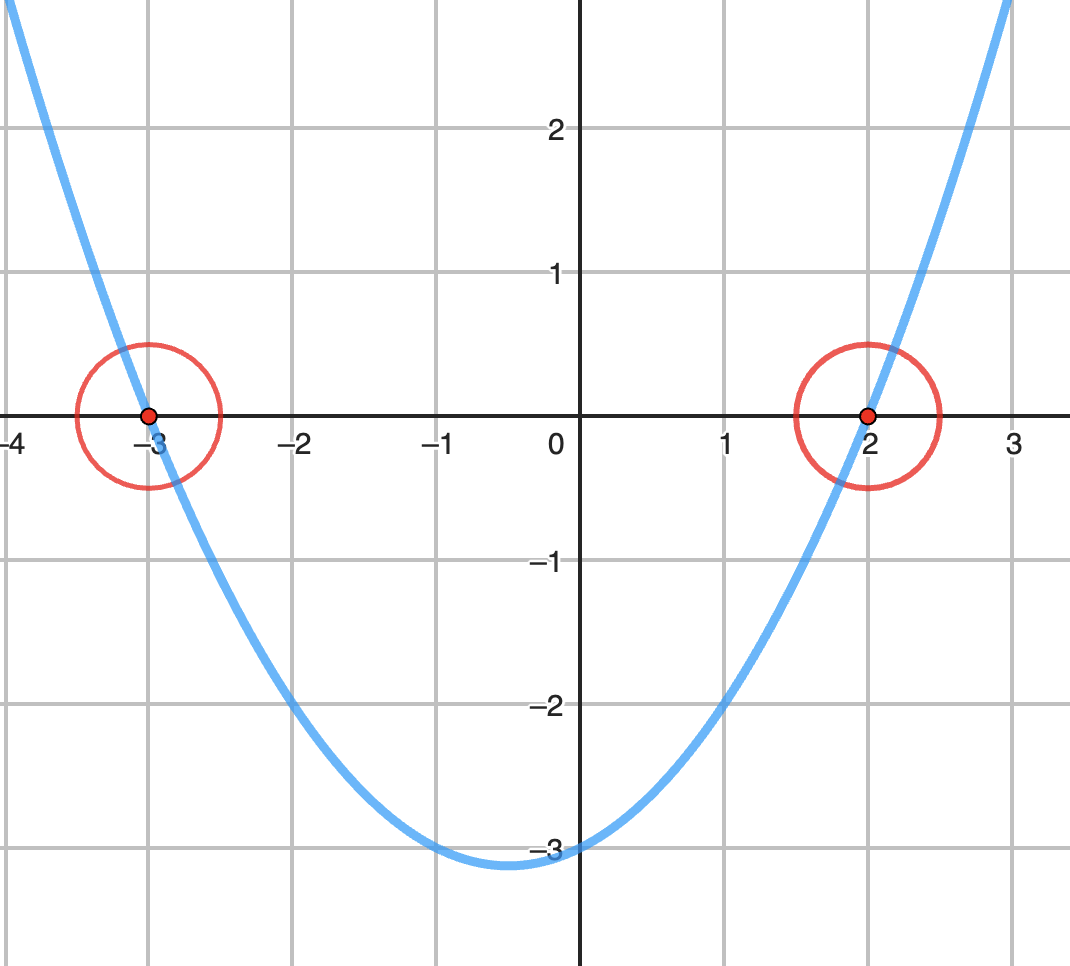
- Les racines sont $x_1$ et $x_2$ → points d’intersection avec l’axe des x
- a > 0 → parabole ouverte vers le haut
- a < 0 → parabole ouverte vers le bas
- Sommet à l’abscisse \( \dfrac{x_1 + x_2}{2} \)
Sur le graphique ci-contre, on peut lire que $x_1 = -3$ et que $x_2 = 2$, et en plus que $a$ est positif, car la parabole est tournée vers le haut.
On peut dire que la forme factorisée sera de la forme: \( f(x) = a(x-x_1)(x-x_2) = a(x-(-3))(x-2) = a(x+3)(x-2) \).