Voici LES formules:
Taux de variation en $a$ : $r(h) = \frac{f(a+h) - f(a)}{h}$.

Le nombre dérivée en $a$ : $f'(a) = \lim_{h\to 0}r(h)$.

Remarque:
Mais que fait cette formule???😨

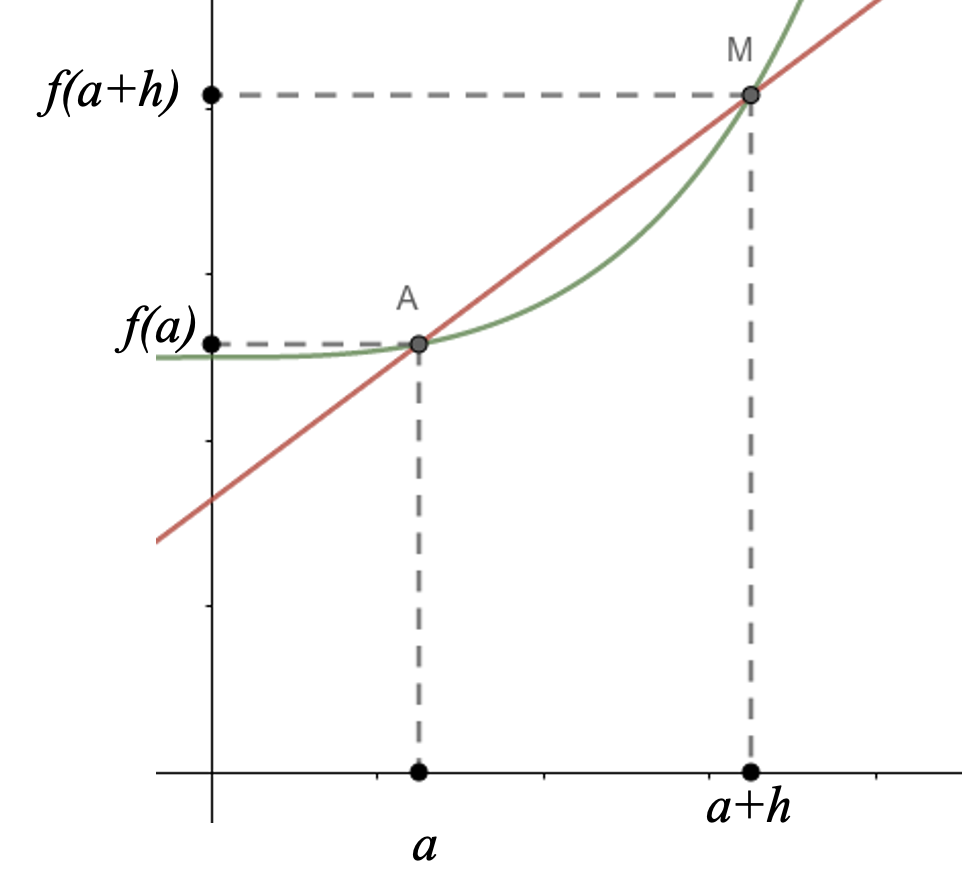
La formule du taux de variation, nous donne la pente de la droite qu'il y a entre le point d'abscisse $a$ sur la courbe et le poit d'abscisse $a+h$ (entre A et M sur le dessin ci-contre).
Le passage à la limite permet de rapprocher le point M du point A, et ainsi, cette droite devient la tangente en A...
Exemple:
Soit \( f(x) = -3x^2 + 2x + 1 \).
Le taux d’accroissement en \( x = 4 \) est :
\[ r(h) = \frac{f(4+h) - f(4)}{h} \]

En développant :
\[ f(4+h) = -3(4+h)^2 + b(4+h) + c = -3(16 + 8h + h^2) + 2 \times 4 + 2h + 1 = -48 - 24h-3h^2+8+2h+1 = -3h^2-22h-39 \]
\[ f(4) = -3 \times 4^2 + 2 \times 4 + 1 = -48 + 8 + 1 = -39 \]
\[ f(4+h) - f(4) = -3h^2-22h-39 - (-39) = -3h^2-22h \]
\[ r(h) = \frac{f(4+h) - f(4)}{h} = \frac{-3h^2-22h}{h} = \frac{h(-3h-22)}{h} = -3h -22 \]

Donc : \( f'(4) = \lim_{h \to 0} r(h) = \lim_{h \to 0} -3h -22 = -22 \)

Cela veut dire que la pente de la tangente à la courbe est de -22 en $x=4$. On a localement, une corube qui baisse fortement.

N'hésitez pas à vérifier votre résultat sur la calculatrice:
- Numworks: Tracer la courbe/Graphique/Boîte à outils/Chercher/Tangente.
- TI : Tracer la courbe/

Tu vas avoir besoin d'un papier et d'un crayon pour ce défi.

Soit \( f \), la fonction définie par :

\( f(x) = 3x^2 - 1x + 2 \)

Calculer :