Le cercle trigonométrique – Tout ce qu’il faut savoir
1. Le cercle de rayon 1
On place un cercle de rayon 1 centré à l’origine.
→ L’abscisse du point = cos de l’angle (nous verrons ça dans le défi2)
→ L’ordonnée du point = sin de l’angle(nous verrons ça dans le défi2)
M(cos θ ; sin θ)
2. Degrés ↔ Radians
| 360° | = | = | 2π | un tour complet |
| 180° | = | = | π | demi-tour |
| 90° | = | = | π/2 | quart de tour |
| 60° | = | = | π/3 | |
| 45° | = | = | π/4 | |
| 30° | = | = | π/6 | |
Pourquoi les radians (et pas les degrés) ?
Parce que 1 radian = longueur d’arc égale au rayon
→ Les formules deviennent magiques et simples :
Dérivée : (cos x)' = −sin x
Longueur d’arc : l = r × θ
Aire de secteur : A = ½ r² θ
En degrés ? Ce serait l’enfer. En radians ? C’est la beauté pure.
Le cercle trigonométrique, c’est ta boussole en maths.
Maîtrise-le → tu maîtrises toute la trigo.
Nous travaillerons principalement avec des angles de la forme $\pi /2$, $\pi /3$, $\pi /4$ et $\pi /6$. Voici leur placement sur le cercle trigo...
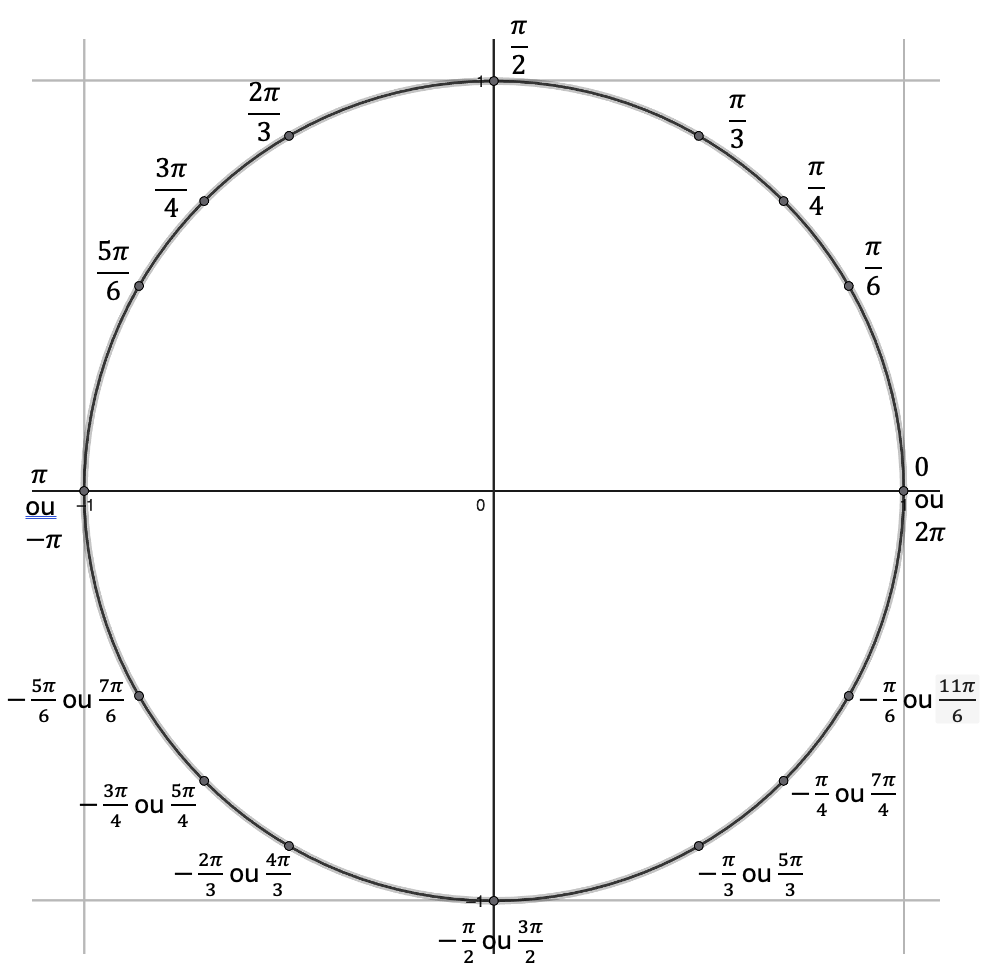Remarque importante:
Un point sur le cercle trigo possède une infinité de valeurs en radian. En effet, si nous prenons $\frac{\pi}{6}$, si on fait un tour (ou plusieurs dans un sens ou un autre), on attérit sur le même point.
Ainsi, $\frac{\pi}{6}$ est au même placement que $\frac{13\pi}{6}$, que $\frac{-11\pi}{6}$, que $\frac{25\pi}{6}$, ...