| Angle \( \alpha \) | \( 0 \) | \( \dfrac{\pi}{6} \) | \( \dfrac{\pi}{4} \) | \( \dfrac{\pi}{3} \) | \( \dfrac{\pi}{2} \) | \( \pi \) |
|---|---|---|---|---|---|---|
| \(\cos \alpha\) | \( 1 \) | \( \dfrac{\sqrt{3}}{2} \) | \( \dfrac{\sqrt{2}}{2} \) | \( \dfrac{1}{2} \) | \( 0 \) | \( -1 \) |
| \(\sin \alpha\) | \( 0 \) | \( \dfrac{1}{2} \) | \( \dfrac{\sqrt{2}}{2} \) | \( \dfrac{\sqrt{3}}{2} \) | \( 1 \) | \( 0 \) |
À connaître par cœur — c’est ta boussole en trigonométrie !
En effet à partir de ces angle et de la connaissance du cercle trigo, tu peux en déduire tous les autres angles de la forme $\pi /2$, $\pi /3$, $\pi /4$ et $\pi /6$.
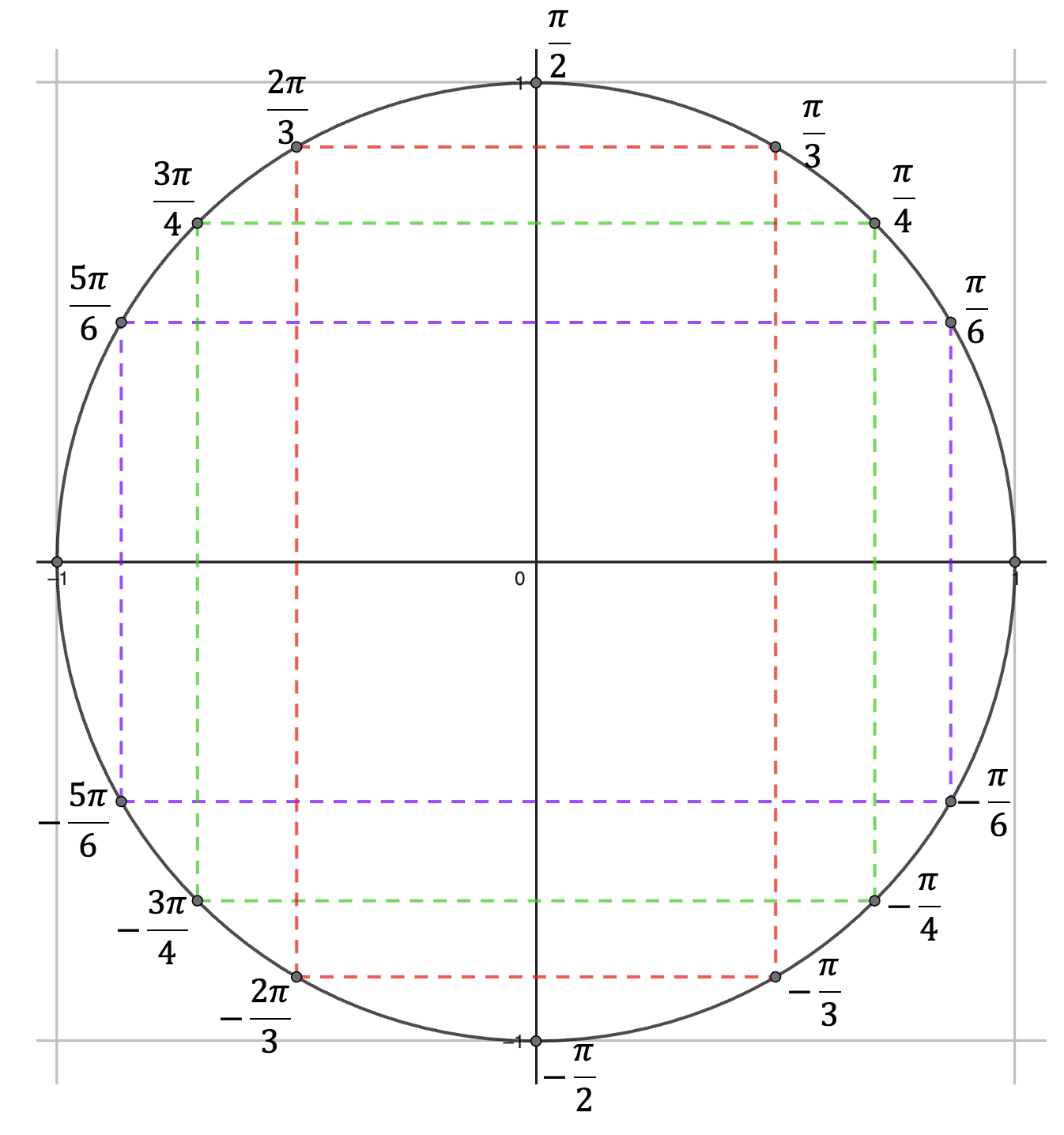
À l'aide du cercle ci-dessus, si tu connais les valeurs de $\cos(\pi /6)$, tu peux trouver celle de $\cos(-\pi /6)$ (c'est la même), ou de $\cos(5\pi /6)$ qui lui est opposée.
À toi de t'entraîner pour maîtriser le cercle trigo!!!💪