Forme factorisée \( f(x) = a(x-x_1)(x-x_2) \)
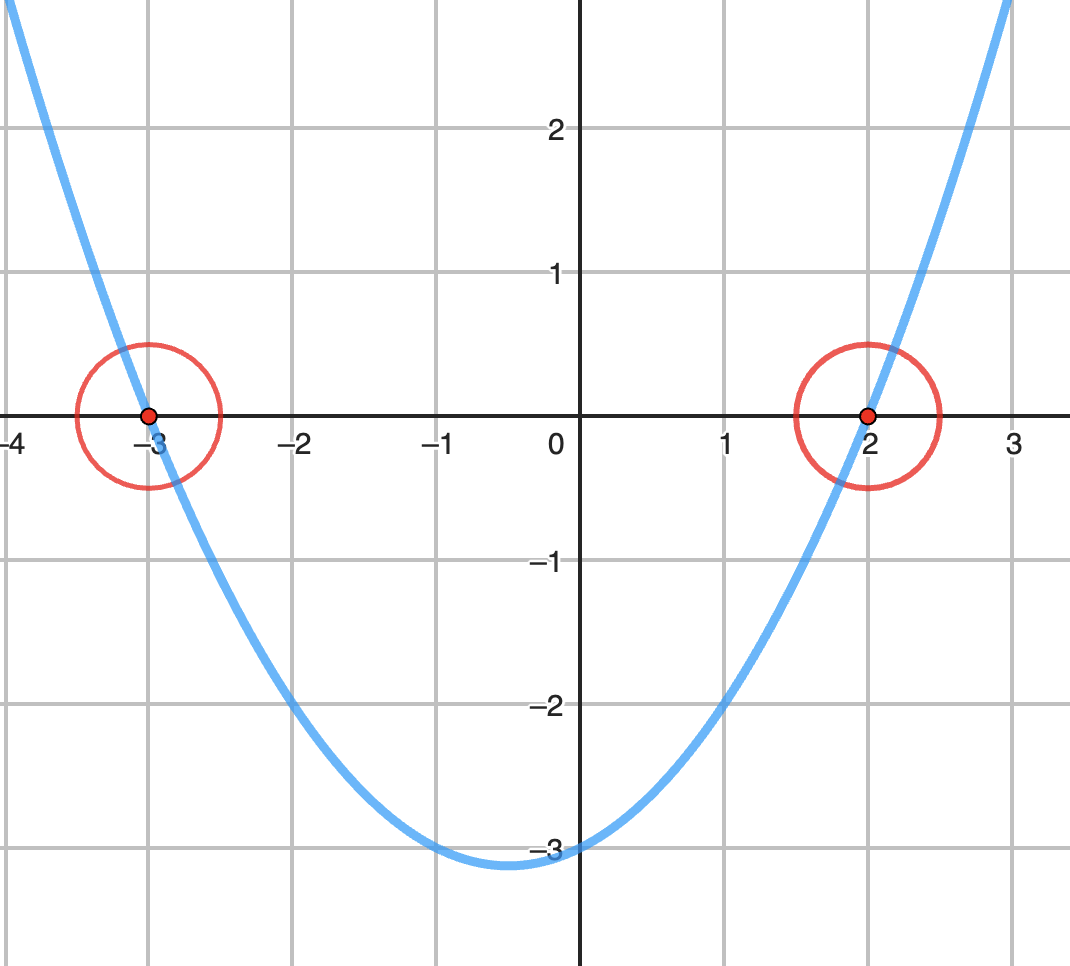
Avec le défi précédent, nous avons appris à lire les racines sur le graphique.
Si on nous donne la forme développée de $f$, on trouver l'intégralité de la forme factorisée facilement.
Avec le graphique suivant, on nous donne en plus le fait que $f(x) = \textcolor{red}{0,5}x^2 + 0,5x - 3$.
Ainsi, on peut dire que $\textcolor{red}{a = 0,5}$ et que les racines sont: $x_1 = -3$ et $x_2 = 2$.
Donc, \( f(x) = a(x-x_1)(x-x_2) = 0,5(x-(-3))(x-2) = 0,5(x+3)(x-2) \).