📚Loi de probabilité

Définition :

$\Omega$ désigne l’univers d’une expérience aléatoire ( l’ensemble des issues possibles) ; on a défini une loi de probabilité sur cet univers. On définit une variable aléatoire X sur Ω lorsque l’on associe un nombre réel à chaque issue.

Exemple :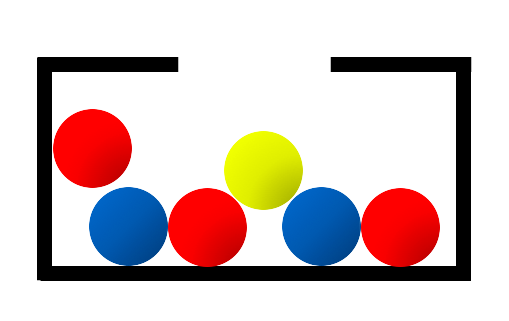

Dans une urne, il y a 3 boules rouges, 2 boules bleues et une boule jaune.
On tire au hasard une boule dans cette urne.
Pour une boule rouge tirée, on gagne 1€, pour une boule bleu, on gagne 3€ et pour une boule jaune, on perd 2€.
On définit ainsi une variable aléatoire X qui prend les valeurs : 1, 3 et -2.
On notera {X= $x_i$} (par exemple {X = 1}) l’événement « la valeur $x_i$, est obtenue »( par exemple « la valeur 1, est obtenue » et {X< $x_i$} l’événement « toutes les valeurs strictement inférieur à $x_i$, sont obtenues ».

Définitions :

• La probabilité de l’évènement ${X=a}$ est la probabilité de l’évènement formé de toutes les issues auxquelles on associe le nombre a. On note $P(X=a)$ cette probabilité.


• Définir la loi de probabilité de la variable aléatoire $X$, c’est associer à chaque valeur $x_i$ prise par $X$ la probabilité de l’évènement $X = x_i$.

On représente généralement la loi de probabilité par un tableau :

Valeurs prises par la variable aléatoire X : $x_i$	$x_1$	...	$x_i$	...	$x_n$
Probabilité associée $P(X = x_i)$	$P(X = x_1)$ ou $p_1$	...	$P(X = x_i)$ ou $p_i$	...	$P(X = x_n)$ ou $p_n$

Remarques :

• La somme des probabilité doit toujours être égale à 1.


• Pour vérifier que vous avez une loi de probabilité, vous devez vérifier que vous avez bien toutes les issues listées dans votre tableau, qu’aucune probabilité n’est négative et que la somme des probabilités fait bien 1.

Dans notre exemple, on obtient le tableau suivant:

Gain ou perte	1	3	-2
Probabilité associée $P(X = x_i)$	$\frac{1}{2}$	$\frac{1}{3}$	$\frac{1}{6}$

Dans un lycée, on analyse le retard des élèves. Ils sont soit à l'heure, soit 5mins en retard, soit 10mins en retard.

On note X la variable aléatoire égale au retard en minutes.

• La probabilité d’avoir 5 minutes de retard est 0.17.
• La probabilité d’avoir 10 minutes de retard est 0.07.

Complétez le tableau ci-dessous en indiquant les valeurs possibles de $X$ rangées dans l'ordre croissant et leurs probabilités associées. Puis répondez aux questions.
Les résultats seront arrondis au centième si besoin.