Le nombre dérivé en un point représente la pente de la tangente à la courbe en ce point.

Petit rappel:

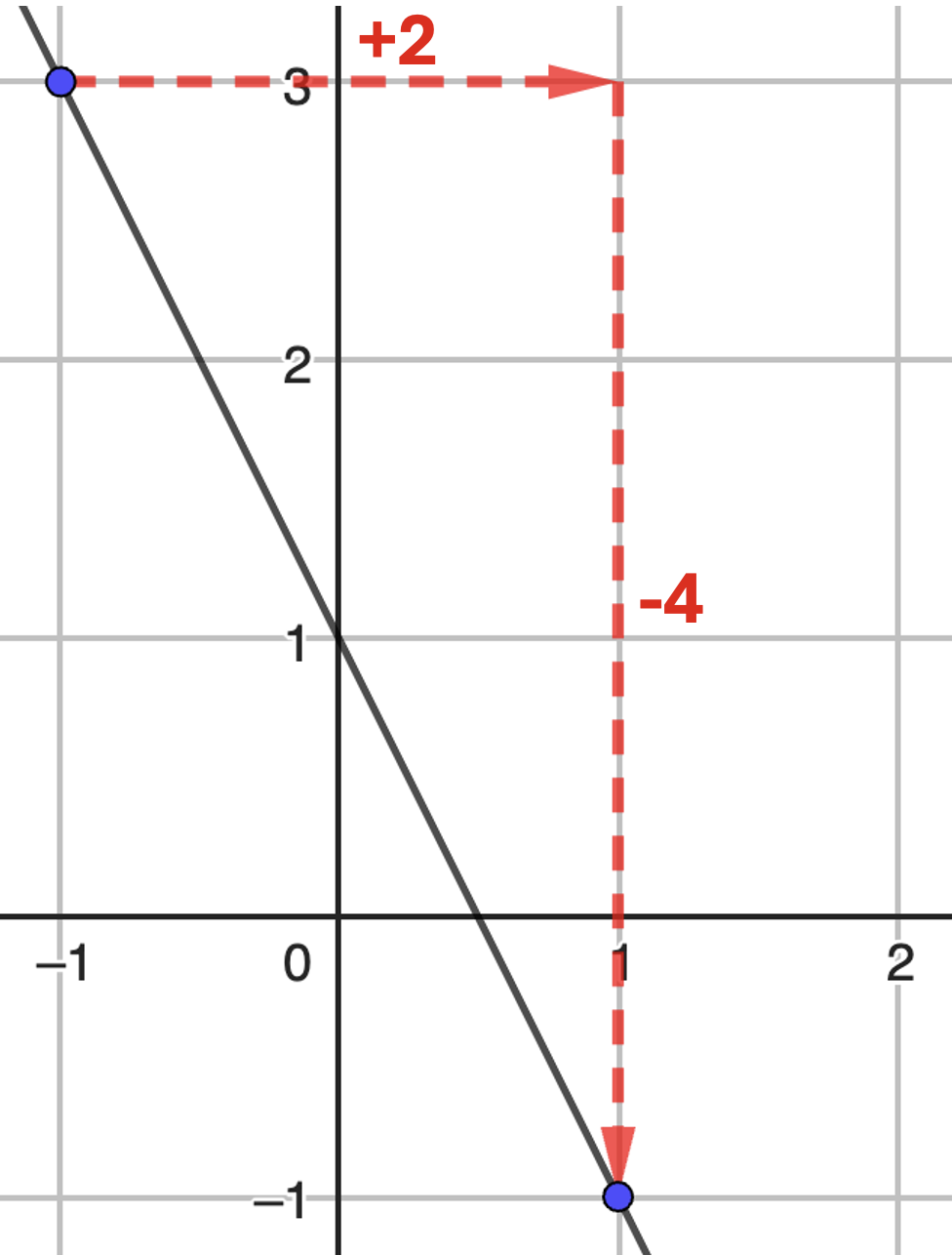
Pour trouver la pente d'une droite, tu cherches 2 points d'intersection entre ta droite et le quadrillage (c'est pour la précision 😉). Puis tu regardes le déplacement horizontal puis vertical pour aller de l'un à l'autre (attention aux signes selon le sens...).

La pente se trouve avec cette petite formule: $ \frac{déplacement ~ vertical}{déplacement ~ horizontal} $.

Dans notre exemple à droite, on voit que la pente est de: $ \frac{-4}{+2} = -2 $. Le nombre dérivé nous donne un renseignement très important sur le comportement de la courbe autour de ce point:
Si le nombre dérivé est positif alors la courbe sera croissante à proximité de ce point, s'il est négatif, elle sera décroissante...