Pour les évolutions successives ou réciproque, nous allons nous servir des coefficients multiplicateurs qui sont très pratiques.

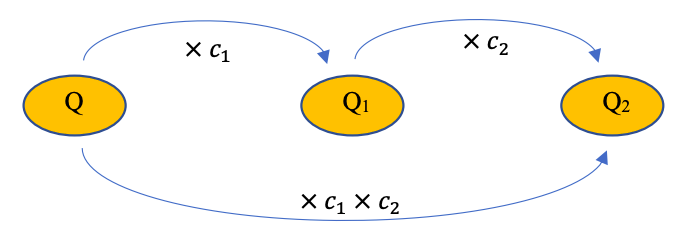
Évolutions successives

Lorsqu’une quantité Q subit plusieurs évolutions successives (augmentations et/ou diminutions), alors le coefficient multiplicateur global est le produit des coefficients multiplicateurs de chaque évolution.

Exemple:
Le prix d'un produit augmente de 20%, puis baisse de 10%.
- Coef. multiplicateur de l'augmentation de 20%: $1 + \frac{20}{100} = 1,2$.
- Coef. multiplicateur de la baisse de 10%: $1 - \frac{10}{100} = 0,9$.

- Coef. multiplicateur global: $1,2 \times 0,9 = 1,08$ soit une augmentation de 8%.

Remarque:
On voit qu'une augmentation de 20% suivie d'une baisse de 10% est équivalent à une hausse de 8% (et non de 10 % 😉 ).

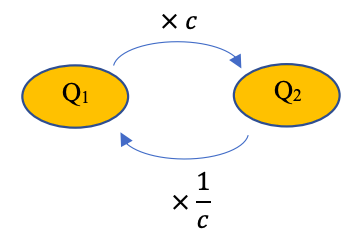
Évolution réciproque

Une quantité Q1 subit une évolution de $t$% pour obtenir une quantité Q2. Le coefficient multiplicateur $c$ de cette évolution vaut : $c = 1 \pm \frac{t}{100}$.
Le coefficient multiplicateur réciproque $c’$ vaut : $c = \frac{1}{c} $.

Exemple:
Le prix d'un produit subit une hausse de 10%.
- Coef. multiplicateur de cette hausse de 10%: $1 + \frac{10}{100} = 1,1$.
- Coef. multiplicateur réciproque de cette hausse: $\frac{1}{1,1} \approx 0,91$ soit une baisse de 9%.
Ainsi une hausse de 10% peut être compensée par une baisse de 9% pour revenir à sa valeur initiale.

Faire ce défi te permettra de bien comprendre la notion d'évolutions successives ou réciproque.

---