Voici les différents ensembles de nombres:

• \(\mathbb{N}\) l’ensemble des nombres entiers naturels : \(\mathbb{N}\) = {0 ;1 ;2 ;3 ;...},
• \(\mathbb{Z}\) l’ensemble des entiers relatifs : \(\mathbb{Z}\) = {.... -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; ....},
• \(\mathbb{D}\) est l'ensemble des nombres décimaux: ils peuvent se mettre sous la forme \(\frac{a}{10^n}\) (nombre fini de chiffres après la virgule).
• \(\mathbb{Q}\) est l'ensemble des rationnels: ils peuvent se mettre sous la forme \(\frac{a}{b}\).
• \(\mathbb{R}\) est l'ensemble des réels. Il est constitué de l'ensemble des nombres que tu connais.

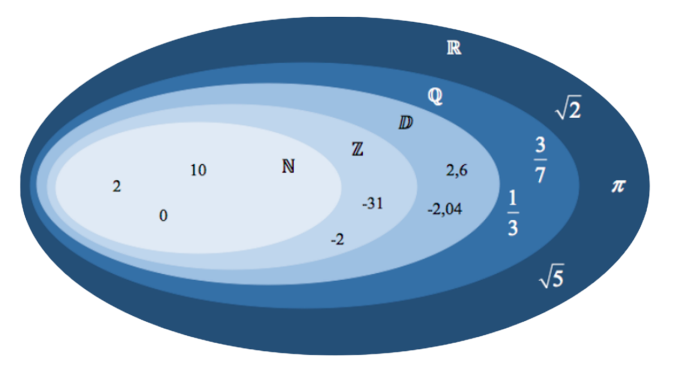
On peut écrire: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{D} \subset \mathbb{Q} \subset \mathbb{R} \) (\(\subset \) signifie est inclu dans)

Quelques exemples pour bien comprendre:

• 2 \(\in \mathbb{N}\),
• \(\sqrt{4} \in \mathbb{N}\) car \(\sqrt{4} = 2\) ,
• \(\frac{1}{3} \in \mathbb{Q}\) car \(\frac{1}{3} \approx 0,3333....\). Il y a une infinité de chiffres après la virgule
• \(\frac{1}{2} \in \mathbb{D}\) car \(\frac{1}{2} = 0,5 = \frac{5}{10} \).