Pour trouver un vecteur directeur d'une droite graphiquement, c'est simple:

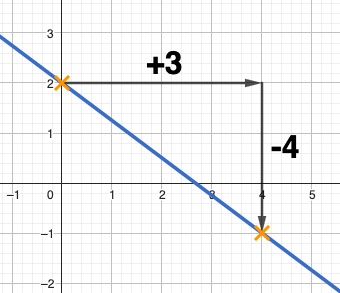
Trouve un point de la droite qui se situe à un croisement du quadrillage, puis trouves-en un autre (ce sont les 2 points oranges sur le graph ci-contre).

Ensuite, tu lis le déplacement horizontal puis vertical, pour passer de l'un à l'autre.

Ici, on trouve un déplacement horizontal de +3, et un déplacement vertical de -4.

Le vecteur directeur est donc: $\overrightarrow{u} (3 ; -4 )$.

Remarque:
Tous les vecteurs colinéaires à ce vecteur sont aussi des vecteurs directeurs de cette droite.
Ainsi: $\overrightarrow{v} (6 ; -8 )$ ou $\overrightarrow{w} (-3 ; 4 )$ sont aussi des vecteurs directeurs de cette droite ($\overrightarrow{v} = 2 \times \overrightarrow{u}$ et $\overrightarrow{w} = -1 \times \overrightarrow{u}$).

---