Vous avez vu ce théorème durant vos années collège, mais il reste encore bien pratique encore et nous le recroisserons cette année.
Voici ce qu'il dit:

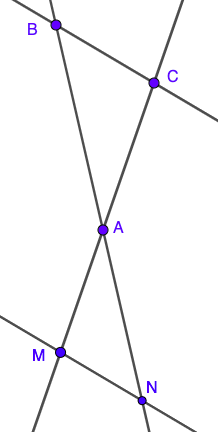
Dans une configuration de Thalès comme ci-contre, avec (BC)//(MN) on a:
$\frac{AB}{AN} = \frac{AC}{AM} = \frac{BC}{NM}$.

Cela peut être utilise pour calculer une longueur

Voyons sur un cas pratique:
Nous gardons la configuration précédente, et on nous donne: AB = 4, AC = 3, AM = 2,5.
On nous demande de calculer AN.

On a: - B, A, N et C, A, M alignés dans le même ordre, - (BC)//(MN)

D'après le théorème de Thalès on a:
$\frac{AB}{AN} = \frac{AC}{AM} = \frac{BC}{NM}$.

$\Leftrightarrow \frac{4}{AN} = \frac{3}{2,5} = \frac{BC}{NM}$.

Avec l'égalité des 2 premières fractions on en déduit:
$ AN = \frac{4 \times 2,5}{3} \approx 3,3$.