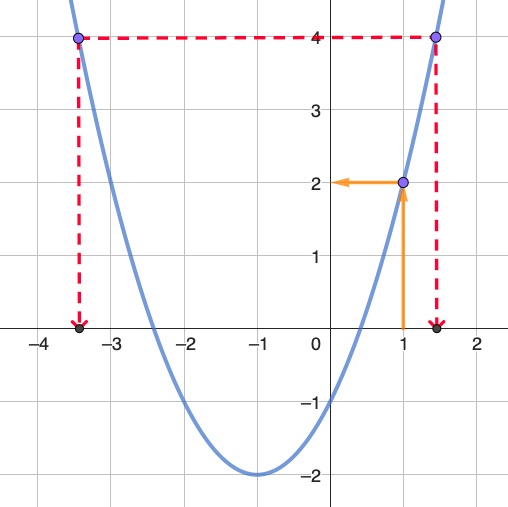
Soit une fonction $ f $ dont on nous donne la représentation graphique ci-contre.
Pour trouver une image ou le(s) antécédent(s) graphiquement, c'est simple, mais il ne faut pas se mélanger
les pinceaux...
Si on veut trouver l'image de 1, ou $ f(1) $ (ce qui est la même chose), il suffit de se placer à 1 sur
l'axe des abscisses, puis rejoindre
la courbe verticalement, et lire sur l'axe des ordonnes l'image (cf. flèches oranges).
Pour trouver le ou les antécédents d'une valeur, par exemple 4, on trace une droite horizontale à $y = 4$,
et on cherche tous les points d'intersections.
Il suffit de lire l'abscisse de chacun de ces points. Ici, on trouve que les antécédents de 4 sont -3,4 et
1,4 (cf. traits rouges).
Remarque: Si il n'y a pas de points d'intersection, alors il n'y a pas d'antécédents.
Soit une fonction $ f $ dont la représentation graphique est donnée ci-dessous:
Réponds au questions suivantes.
Si il n'y a pas d'antécédent, tu réponds: "rien" (en classe, tu utiliserais le symbole
ensemble vide: $ \emptyset $), si il y a 2 antécédents, par exemple 2 et 3, tu réponds: 2 et 3.
Tu peux te déplacer sur le graphique et zoomer si besoin...