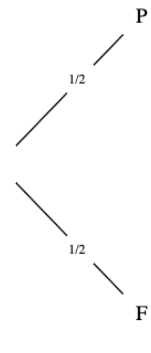
L'arbre des possibles est un outil essentiel pour modéliser (représenter) une situtation de probabilité.
Tu vas devoir apprendre à bien le représenter et bien le compléter.
Prenons, un exemple simple: On lance une pièce non truquée et on regarde si, lorsqu'elle tombe, la face
supérieur est pile (P) ou face (F).
On sait très bien que chaque issue (résultat) à 1 chance sur 2 de se produire soit une probabilité de
$\frac{1}{2}$.
Cela nous donne l'arbre ci-contre.
Pour une expérience de ce type, l'arbre n'est pas très utile, car on peut facilement se représenter cela
de tête.
 Complexifions les choses:
Complexifions les choses:
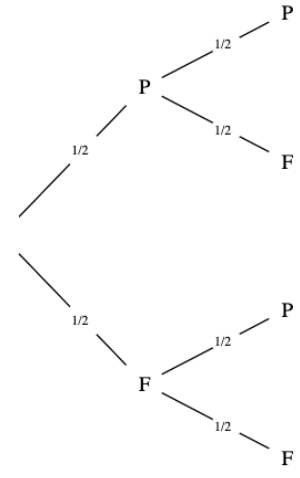
On va lancer notre pièce 2 fois de suite.
Notre arbre va gagner un étage pour représenter ce nouveau tirage.
On voit sur l'arbre ci-contre le nouveau niveau apparaître.
Remarques:
- Les probabilités doivent être mise sur les branches. Vous pourrez les écrire sous forme d'une fraction ou
d'un nombre décimal (pour les cas du type 1 chance sur 3, je te conseille
de préférer la fraction pour ne pas faire d'arrondi).
- la somme des probabilités des branches qui partent d'un point fait 1.
Voyons un exemple d'exercice plus concret et complexe:
Sur la planète Alphabetagamma, on trouve 2 types d'individus: les Gaussiens et les Pythagoriciens.
On sait que 45% des individus sont des Gaussiens.
Parmi les Gaussiens, on sait que 35% ont les yeux violets, le reste ont les yeux jaunes.
Chez les Pythagoriciens, on sait que 60% ont les yeux violets, le reste ont les yeux jaunes.
On choisit au hasard un individu de cette planète.
Soit $A$, l'évènement: l'individu est un Gaussien,
et $B$, l'évènement: l'individu a les yeux violets.
On nous demande de représenter ce tirage par un arbre...
Correction:
On voit que nous avons 2 caractèristiques: Gaussiens/Pythagoriciens et yeux violets/yeux jaunes.
Nous aurons donc 2 étages à notre arbre.
Pour le premier niveau, il y a 2 issues possibles: Gaussiens ou Pythagoriciens, donc $A$ ou $\overline{A}$
(qui est le contraire de A).
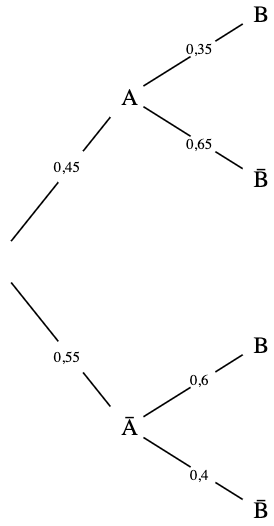
On sait que 45% des individus sont des Gaussiens, donc $p(A)=0,45$. On en déduit que la probabilité qu'il
soit Pythagoriciens, donc $p(\overline{A}) = 1 - 0,45 = 0,55$.
Pour le second niveau, si on a tiré au sort un Gaussien, on sait qu'il y a 35% de chance qu'il ait les
yeux violets. Donc la probabilité qui ira de $A$ à $B$ sur notre abre sera de 0,35.
On peut en déduire facilement, qu'il y a donc 65% de chance qu'il ait les yeux jaunes. La probabilité
allant de $A$ à $\overline{B}$ est de 0,65.
On fait de même avec les Pythagoriciens (branches qui partent de $\overline{A}$) et on obtient l'arbre
ci-contre.
Dans une entreprise intergalactique, il y a 70 % de femmes, les autres sont
des hommes.
Parmi les de femmes, 20 % ont une crête verte, et parmi
les hommes, 30 % ont une crête verte.
On choisit au hasard un individu.
On nomme $F$, l'évènement: l'individu choisit est une femme,
et $V$ l'évènement: l'individu a une crête verte.
Compléter l'arbre ci-dessous.
Vos résultats seront donnés sous forme de nombre décimal arrondi au centième.