Dans le défi 1, nous avons vu comment compléter un arbre des possibles, nous allons voir maintenant comment l'utiliser.

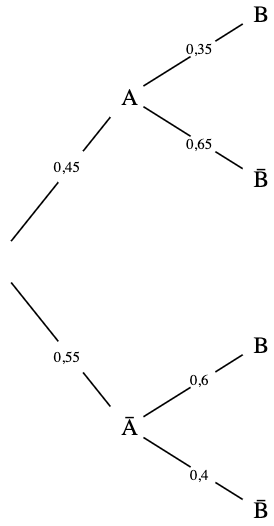
Nous avons l'arbre ci-contre.

Nous voyons qu'il y a 4 chemins: $A/B, A/\bar{B}, \bar{A}/B$ et $\bar{A}/\bar{B}$.

Ils nous permettent de trouver les probabilités d'évènements d'intersection. Ainsi, le premier chemin, nous donnera la propabilité: $p(A \cap B)$.

Pour la calculer, c'est simple, il suffit de multiplier les probabilités des branches de ce chemin. On trouve: $p(A \cap B) = 0,45 \times 0,35 = 0,1575$.

Maintenant, si tu veux calculer $p(A)$, il suffit d'additionner les probabilités de tous les chemins qui mènent à $A$. Ici, il n'y en a qu'un, donc $p(A) = 0,45$.

Si tu veux trouver $p(B)$, tu additionnes les probas de tous les chemins qui mènent à $B$.
Ici, il y en a 2. On peut écrire:

$p(B) = p(A \cap B) + p(\bar{A} \cap B) = 0,45 \times 0,35 + 0,55 \times 0,6 = 0,4875$.

À toi de jouer...

---