Un vecteur est caractérisé par:
- sa longueur,
- sa direction,
- son sens.
Ainsi, si 2 vecteurs sont égaux, alors, ils ont la même longueur, la même direction et le même sens.
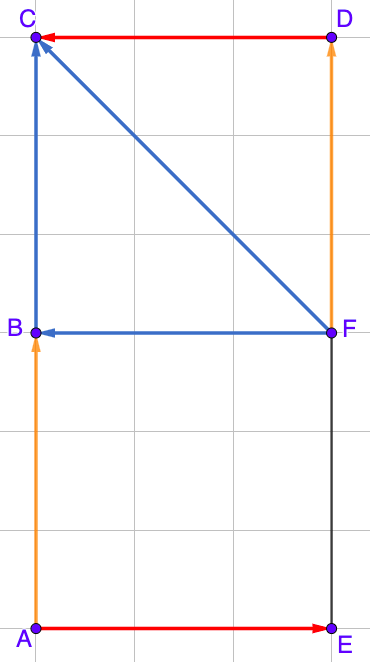
Sur la figure ci-contre, on a:
$\overrightarrow{AB} =
\overrightarrow{FD}$.
Des vecteurs opposés ont la même longueur et la même direction mais des sens opposés.
Sur la figure ci-contre,
$\overrightarrow{AE}$ et
$\overrightarrow{DC}$ sont opposés.
On peut écrire:
$\overrightarrow{AE} = -\overrightarrow{DC}$.
Remarque utile: On a : $\overrightarrow{AB} = -\overrightarrow{BA}$.
Pour la somme de vecteurs, on peut la voir comme une indication de trajet.
Pour aller de F à C (
$\overrightarrow{FC}$), on peut passer par B: (
$\overrightarrow{FB} + \overrightarrow{BC}$). On a donc:
$\overrightarrow{FC} = \overrightarrow{FB} + \overrightarrow{BC}$.
Avec les égalités de vecteurs, on peut aussi écrire: $\overrightarrow{FC} = \overrightarrow{FB} +
\overrightarrow{BC} = \overrightarrow{DC} + \overrightarrow{BC}$
