Parité d'une fonction

	Fonction paire	Fonction impaire
Définition	Une fonction f , définie sur un ensemble $\mathcal{D} f$ est paire lorsque : Pour tout $x \in \mathcal{D} f$ , $f(-x)=f(x)$. Exemple : Montrer que la fonction définie sur $\mathbb{R}$ par $f(x)=x^{4}$ est paire. Pour tout $x \in \mathbb{R}$, $f(-x)=(-x)^{4}=x^{4}=f(x)$. Ainsi $f$ est paire.	Une fonction $f$, définie sur un ensemble $\mathcal{D} f$ est impaire lorsque : Pour tout $x \in \mathcal{D} f$ , $f(-x)=-f(x)$. Exemple : Montrer que la fonction définie sur $\mathbb{R}$ par $f(x)=x^{3}$ est impaire. Pour tout $x \in \mathbb{R}$, $f(-x)=(-x)^{3}=-x^{3}=-f(x)$. Ainsi $f$ est impaire.
Représentation graphique	Dans un repère orthogonal, la courbe représentative d’une fonction paire est symétrique par rapport à l’axe des ordonnées.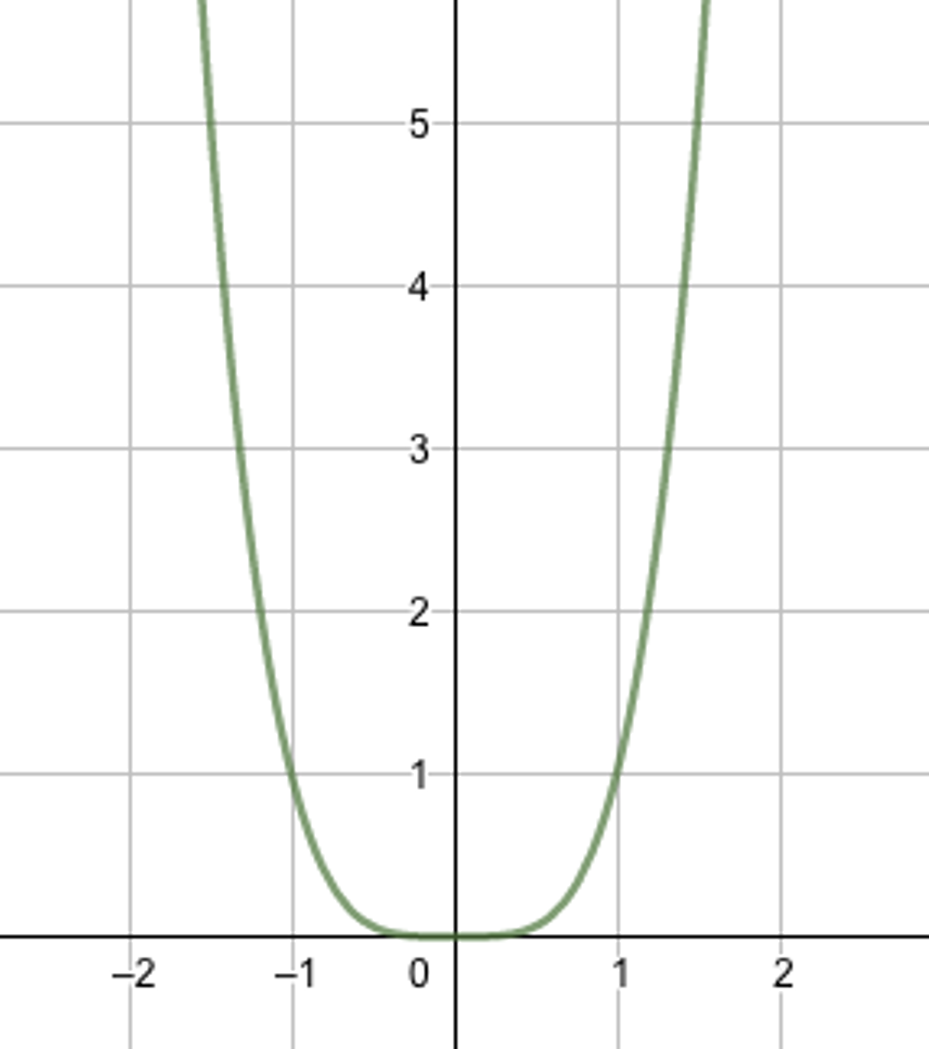	Dans un repère orthogonal, la courbe représentative d’une fonction impaire est symétrique par rapport à l’origine du repère.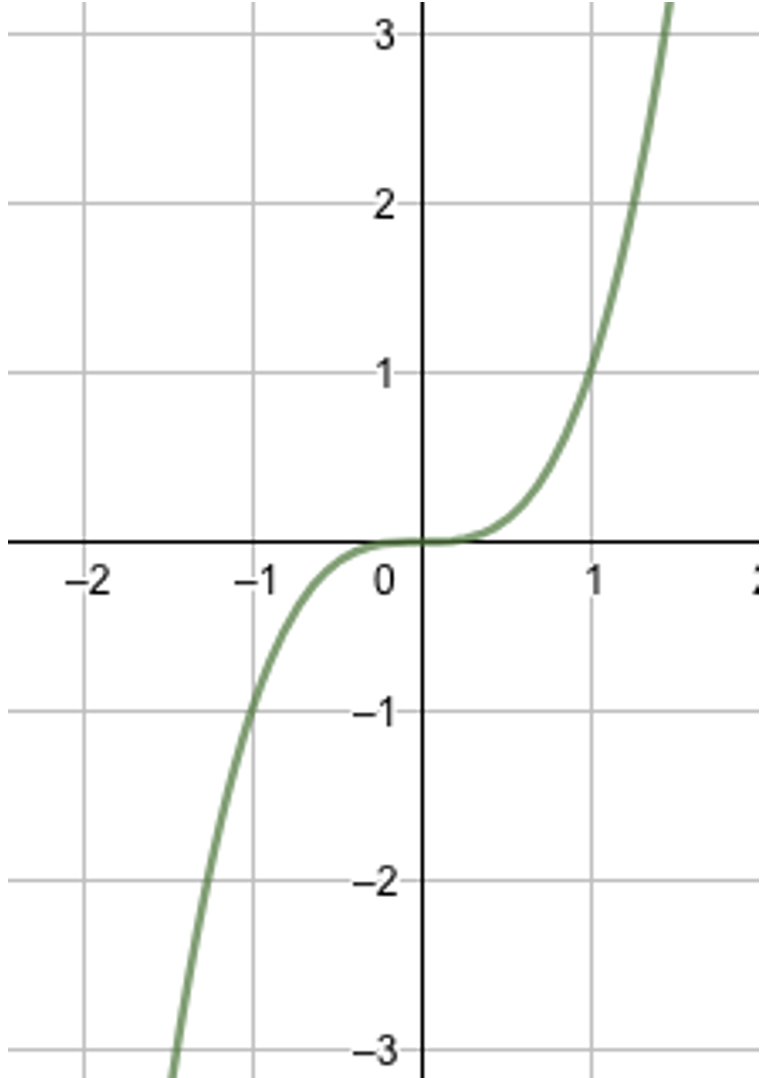

Remarques :

Étudier la parité d’une fonction revient à déterminer si elle est paire, impaire ou ni paire, ni impaire.
La fonction nulle est la seule fonction qui soit à la fois paire et impaire.
si $n$ est pair alors $(-x)^{n}=x^n$ et si n est impaire alors $(-x)^{n}=-(x)^{n}$.

Soient 3 fonctions dont on donne la représentation graphique ci-dessous :

Questions

1. La courbe bleue représente une fonction car elle est symétrique par rapport à .

2. La courbe rouge représente une fonction car elle est symétrique par rapport à .

3. La courbe orange représente une fonction car elle est symétrique par rapport à .