Méthode pour étudier une fonction de degré 2
- Calculer \( f'(x) \):
Ici, tu obtiendras tout le temps une fonction dérivée de degré 1 de le forme $f'(x)=ax+b$, dont on va
étudier le signe.
- Trouver la racine de \( f'(x) = 0 \):
Facile 😉: la racine est $x_0 = -\frac{b}{a}$.
- Étudier le signe de \( f'(x) \):
Easy aussi 😁: signe de -a | 0 | signe de a.
- Déduire la variation de \( f \):
Que dire... si $f'(x)$ est positif alors la fonction est croissante (↗) sinon il est positif, la fonction
est décroissante (↘).
- Calculer \( f(x_0) \)
Exemple:
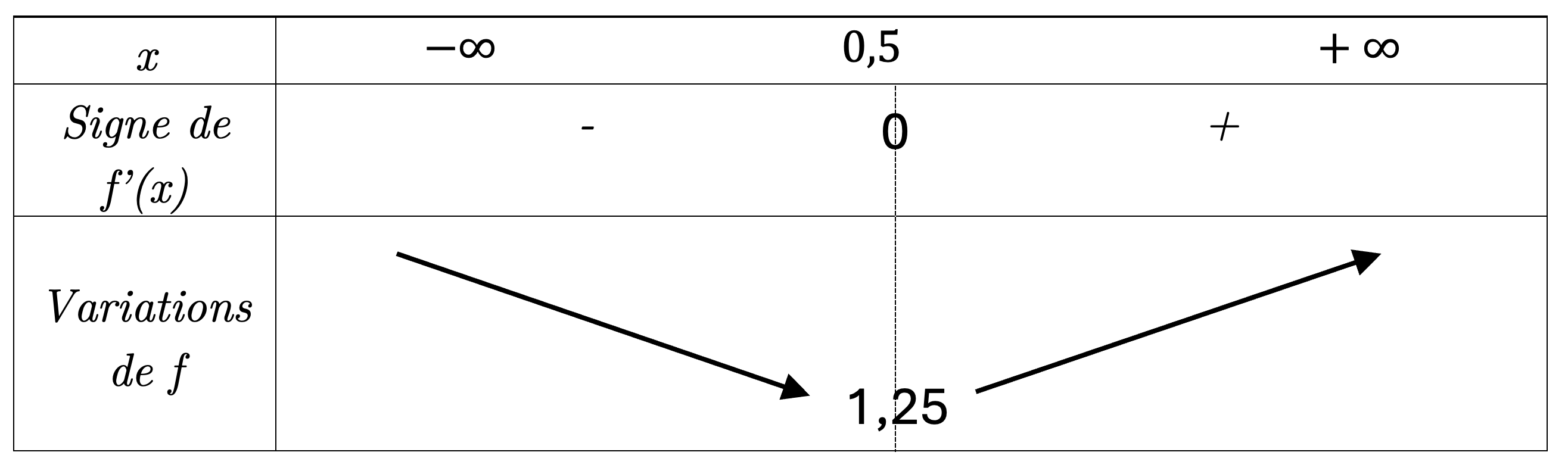
Prenons la fonction définie sur $]-\infty; +\infty[$ par $f(x)= 3x^2 - 3x + 2$.
- $f'(x)= 6x - 3$.
- La racine: Ici, on a $a = 6$ et $b = -3$ (⚠️ aux signes...), donc $x_0 = -\frac{-3}{6} = 0,5$.
- Signe de $f'(x)$: On sait que ça sera: signe de -a | 0 | signe de a, donc: - | 0 | +
- $f(0,5) = 1,25$
On obtient le tableau suivant: