📌 📌 Le coefficient binomial
Le coefficient binomial permet de compter le nombre de façons différentes
d’obtenir k succès parmi n essais.
\[
\binom{n}{k}
\]
- \(n\) : nombre total d’essais
- \(k\) : nombre de succès
On le rencontre :
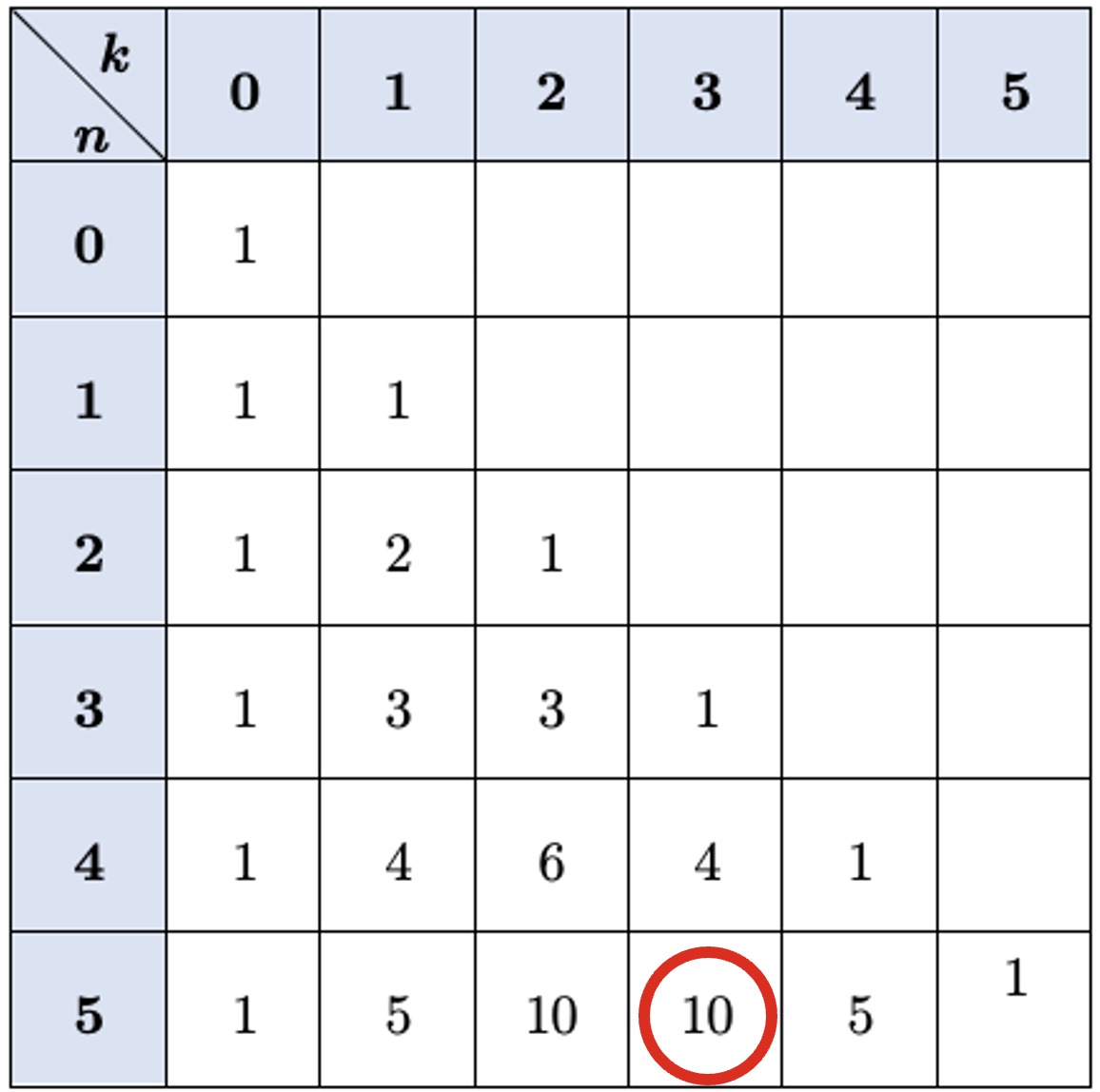
- dans le triangle de Pascal
- avec la touche nCr de la calculatrice ou boite à outils/Proba/dénomb
- pour compter des chemins dans un arbre
Exemple :
\( \binom{5}{3} = 10\) :