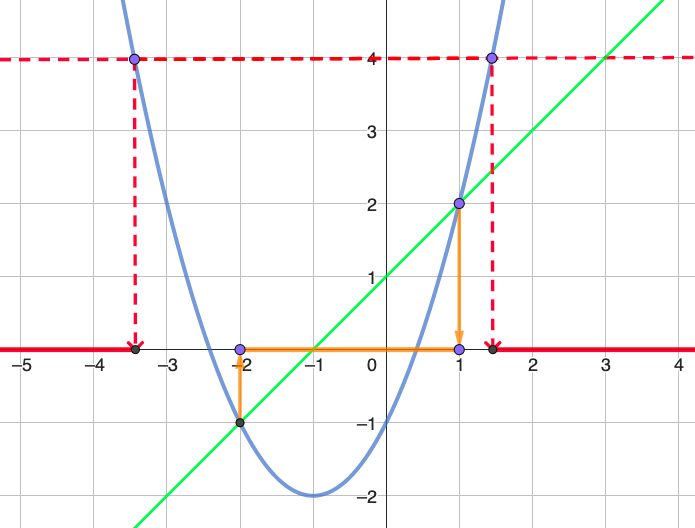
Soit une fonction $ f $ (bleue) et une fonction $ g $ (verte) dont on nous donne les représentations
graphiques ci-contre.
Pour résoudre graphiquement l'inéquation $ f(x) > 4 $, on va donner un sens graphique à cette
inégalité.
Graphiquement, cela veut dire que nous allons chercher les endroits où la fonction $f$ est
strictement au au-dessus de la droite horizontale $ y = 4 $.
Avec les traits rouge, nous voyons que c'est de - infini jusqu'à -3,4 puis de 1,4 à + infini. Comme
nous voulons qu'elle soit
strictement en-desous, nous allons exclure -3,4 et 1,4.
Nous avons donc: $ S = ]-\infty ; -3,4] \bigcup [1,4 ; +\infty[ $.
Pour résoudre $ f(x) \leq g(x) $, nous allons faire la même chose:
Nous voulons trouver les $ x$ où la fonction $f$ (bleue) est en-dessous ou touche la fonction $g$
(verte).
À l'aide des traits orange, nous trouvons: $ S = [-2 ; 1]$.
On voit que la difficulté va surtout être dans la notation sous forme d'intervalle. Il est
essentiel que tu sois à l'aise avec cela ;)
Si ce n'est pas le cas, je te conseille ce défi: Intervalles...